반응형
문제분석:
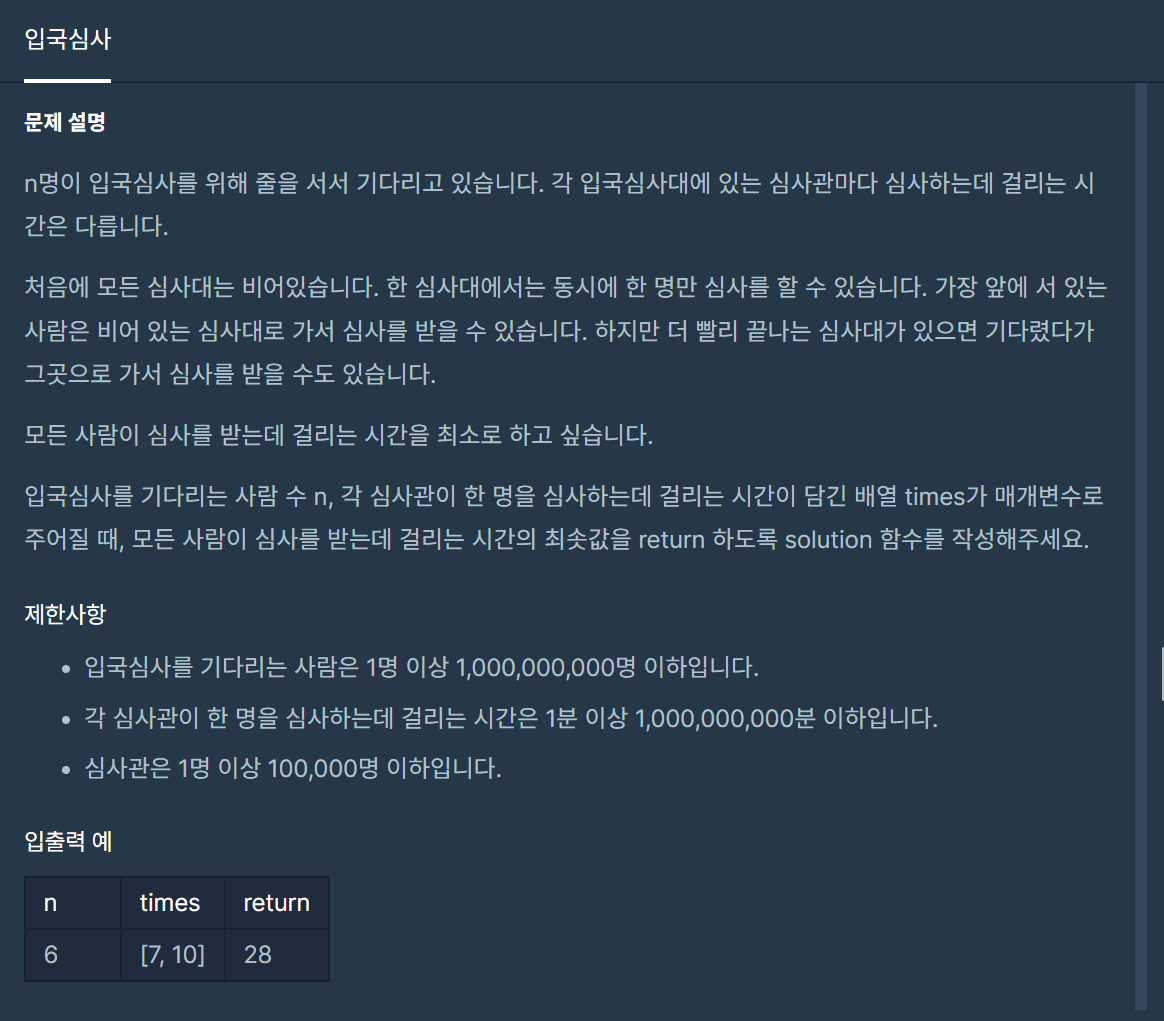
입국심사 게이트가 있는데 게이트마다 심사하는 시간이 다르다.
그리고 그 심사하는 시간이 최소가되는 시간을 구해달라 라는 문제다.
제한사항을 보면 사람과 심사시간의 주어진 수가 심상치않게 크다.
이 문제는 이분탐색을 사용해야만한다.
이분탐색이 무엇이냐?
UP 앤 Down 게임이라고 생각하면 쉽다.
1~ 100 중에서 출제자는 랜덤한 숫자를 하나 고른뒤
맞추는 사람은 1~100숫자중에 랜덤한 숫자를 하나고르는 행위다.
만약 맞추는 사람이 50을 부르면, 출제자의 숫자가 1~49이면 Down , 51~100이면 UP을 외쳐야한다.
이 과정을 출제자의 숫자가 나올때까지 계속 반복하는 게임이다.
이분탐색이 이 알고리즘과 100%동일하다.
UP 앤 DOWN의 원리대로 한번 구현해보자.
최소값을 0, 최대값을 [가장 오래걸리는 심사시간]* 전체인원수로 셋팅하자.
이분탐색을 최고효율로 뽑으려면 당연히 mid =최대값+최소값/2 인값을 탐색해야한다.
mid값의 시간에 모든 사람을 심사할수있다면 -> Down (더 낮은시간으로 모든 사람을 심사할수있는지 확인)
mid의값이 모든사람을 심사할수 없다면 ->UP (시간이부족하므로 심사시간 증가)
Down일때, mid이상의 값들은 필요가 없으므로 Max값을 mid-1로 수정해야한다.
UP일땐, mid 이하의 값들은 필요가 없으므로 Min값을 mid+1로 수정해야한다.
그리고 min 과 max가 동일한다면 멈추면된다.
문제풀이
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
import java.util.*;
class Solution {
public long solution(int n, int[] times) {
long answer = 0;
Arrays.sort(times);
long left=0;
long right=(long)times[times.length-1]*n;
while(true){
if(left>right){
break;
}
long mid=(left+right)/2;
long sum=0;
for(int data:times){
sum+=(mid/data);
}
if(sum<n){
left=mid+1;
}
else{
right=mid-1;
answer=mid;
}
}
return answer;
}
}
|
cs |
반응형
'알고리즘 > 프로그래머스 Level3' 카테고리의 다른 글
| [프로그래머스,Java] Level3: 단어 변환 (0) | 2022.08.05 |
|---|---|
| [프로그래머스,Java] Level3: 선입 선출 스케줄링 (0) | 2022.07.30 |
| [프로그래머스,Java] Level3: 베스트앨범 (0) | 2022.07.13 |
| [프로그래머스,자바] Level3: 추석 트래픽 (0) | 2022.02.13 |
| [프로그래머스,Java] Levle3: 위클리챌린지 11주차[아이템 줍기] (1) | 2021.10.19 |