
문제분석
되게 심플한 문제설명과는 달리, Level2 치곤 (본인이 느끼기엔) 매우 높은 구현난이도를 가지고 있다.
문제 설명에서 '1924를 수 두 개를 제거해 {19,12,14 ...} 를 만들수 있습니다' 를보고
오.. 이 문제는 조합 알고리즘(백트래킹) 써서 만들면 되는구나..
-> 하는 순간 당신은 함정에 빠지는겁니다
이 문제의 제한사항을 보시면 number자리수가 100만자리입니다.
조합을 쓰면.. 1,000,000C2 라는 연산을 하는데 당연히 효율성 펑크나겟죠..?
요점은 무엇이냐! 최대 시간복잡도 O(N)으로 짜야한다는점.
근데 사실 100만번도 많아요... 더줄여야해요 .. O(log(N))을 노력합시다.
풀이전략:
어찌댓든 저희 목표는 제거해서 남는 숫자를 담아야합니다.
즉 반복문을 사용할건데, 전체길이-K(제거한뒤 남는숫자) 만큼 반복을 할겁니다.
이렇게 하시면은 0~K+1중에는 최소 1개는 제거해서 남는 숫자가 존재한다는겁니다.
더 쉽게말하면
0~K+1
1~K+1+1
2~K+1+2
3~K+1+3
4~K+1+4
에서 제거해서 남는숫자가 존재 한다는겁니다.
제거해서 남는숫자는 어떻게 판별할까요?
바로 max값 < idx숫자인 지점의 숫자가 제거해서 남는 숫자입니다.
여기서 max값은 매번 0으로 초기화를 해주셔야합니다.

예시를 통해볼까요해당 예시의 K는 4입니다.
1)0~5 의 구간을 탐색한 결과 41772가 나옵니다.41772에서 max값 < idx숫자인 지점은 7입니다. 제거해서 남는숫자는 '7' 이 존재합니다.
그러면 7을 담고 다음 반복으로 넘어갑니다.
원래는 1~6을 탐색해야하지만, 더 줄여봅시다.
->이전 반복에서 '7'의 idx는 2입니다. 그러면 2까진 탐색할 필요가 없죠. 3부터 탐색해도 전혀 문제가없습니다.
->탐색 Start만 손을봅니다. 탐색 End값은 그대로 유지시킵니다.
2)
즉, 3~6을 탐색합시다.
"725"입니다. 725중 max값 < idx숫자인 지점은는 '7'입니다.
'7'을 담고 다음 스텝으로 넘어갑니다.
3)
본래라면, 2~7을 탐색해야하지만, 앞에서 탐색구간을 줄여놨죠(초기 탐색 Start지점)?
즉 4~7을 탐색합시다.
"252"입니다. 252 중 max값 < idx숫자인 지점은 '5'입니다.
->여기서 또, 탐색구간을 줄일수가있죠 idx 5까지 탐색할필요가 없습니다.
4)
본래라면 3~8을 탐색해야하지만, 앞에서 탐색구간을 줄여 6~8까지 탐색해도됩니다.
즉 "28"입니다. 28 중 max값 < idx숫자인 지점은 "8" 입니다.
-> 여기서 또 , 탐색구간을 줄일수 있습니다. idx는 7까지 탐할필요가 없습니다.
5)
본래라면, 4~9를 탐색해야하지만, 앞에서 탐색구간을 줄여 8~9까지 탐색해도됩니다.
즉 "4" 입니다. max값 < idx숫자인 지점은 "4"입니다.
어처피 단 1개만 탐색할게없네요 여기부터 계속 반복을해가면
775841이 나오게됩니다.
----------------------------------------------------------------------------------------------------
대충 흐름이 잡히셧나요?
요약하자면
1. 제거해서 남는숫자만큼 반복을한다.
2. K+1개만큼 구간을 만들어 탐색한다.
3. max값 < idx숫자인 지점을 파악하고 숫자를 남긴다. 그리고 동시에 탐색구간을 갱신한다
여기까지만 하셔도 테스트는 통과하시겠지만 꼭 4번작업도 하셧으면 좋겟습니다.
4. max값이 9라면 반복을 종료하고 그냥 남긴다
그 이유는...
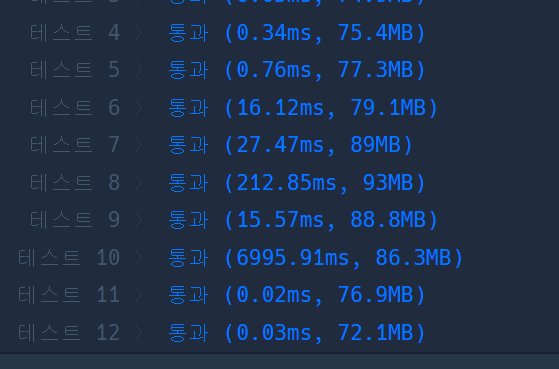
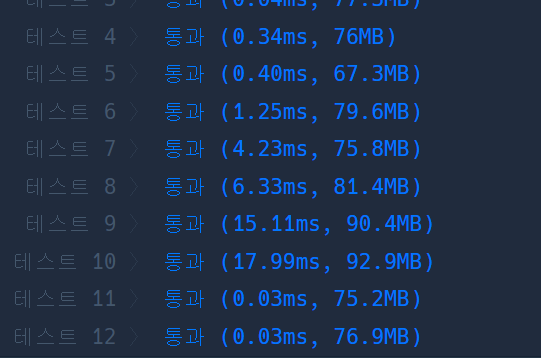
테스트 10번을 보시면 아시겟지만 몇백배는 연산이 줄었습니다.
당연한 이야기지만, max가 9면 9보다 큰 숫자는없으니 탐색할 필요도없이 바로 나와도 됩니다.
문제풀이
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public String solution(String number, int k) {
StringBuilder sb = new StringBuilder();
int idx = 0;
int number_len = number.length();
int max;
// 제거안할 숫자 뽑아내기
for(int i=0; i<number_len - k; i++) {
max = 0;
//0~k+1까지 탐색하고 가장큰 max값 구함
for(int j = idx; j<= k+i; j++) {
int tmp = number.charAt(j)-'0';
//찾아냈으면, max갱신과 max발생지점 다음idx로 탐색 초기지점 설정
if(max < tmp) {
max = tmp;
idx = j+1;
}
//4번 작업도 꼭 해줍시다.
if(max==9){
break;
}
}
//max값입력
sb.append(max);
}
return sb.toString();
}
}
|
cs |
'알고리즘 > 프로그래머스 Level2' 카테고리의 다른 글
| [프로그래머스,자바] Level2: 주차 요금 계산 (2) | 2022.01.19 |
|---|---|
| [프로그래머스,자바] Level2: K진수에서 소수 개수 구하기 (0) | 2022.01.18 |
| [프로그래머스,Java] Level2: 카펫 (0) | 2021.12.18 |
| [프로그래머스,Java] Level2: H-Index (0) | 2021.12.17 |
| [프로그래머스,Java] Level2:다리를 지나는 트럭 (0) | 2021.12.15 |